رگرسيون چيست؟
رگرسيون يعني بازگشت. يعني پيش بيني و بيان تغييرات يک متغير بر اساس اطلاعات متغير ديگر.
مثال: رابطه بين قد و وزن انسانها را در نظر بگيريد. همه مي دانيم که اين رابطه يک رابطه مستقيم رياضي و صد درصدي نيست که لزوما هر که قد بلندتري داشته باشد وزن بيشتري داشته باشد، اما مي توان گفت که با احتمال قابل قبولي افراد با قد بلندتر، وزن بيشتري نيز دارند. در اينجا پيش بيني وزن از روي قد و بيان ارتباط بين اين متغير با روش آماري رگرسيون خطي صورت مي پذيرد که اين رابطه را به صورت کمي به ما نشان مي دهد.
رگرسيون را با معادله رگرسيون بيان مي کنند. در مثال فوق معادله رگرسيون خطي مي تواند به صورت زير باشد:
متغير وزن = متغير قد * b + a
ترسيم اين خط پس از محاسبه ضرايب a و b ما را به خط رگرسيون مي رساند.
همبستگي و رگرسيون
اينکه ما مي توانيم از رگرسيون متغير y بر روي متغير x صحبت کنيم به دليل همبستگي بين دو متغير مي باشد. بنابراين مفهوم همبستگي نيز در اينجا اهميت دارد.
همبستگي يعني تغيير در y چقدر بر روي تغيير بر x تاثير مي گذارد. به عبارت ديگر تغيير در يک متغير چقدر با تغيير در متغير ديگر هماهنگ است. مثلا تغيير در قد چقدر با تغيير در وزن هماهنگي دارد. در اين مثال بديهي است که همبستگي مثبت است. زيرا معمولا افراد قد بلندتر داراي وزن بيشتري مي باشند.
همبستگي را با ضريبي به نام ضريب همبستگي پيرسون اندازه گيري مي کنند که عددي بين صفر و يک است. هر چه مقدار همبستگي به عدد يک نزديک تر باشد، همبستگي بين دو متغير بيشتر است و هر چه به صفر نزديک تر باشد، همبستگي کمتر خواهد بود. همبستگي برابر يک يعني رابطه خطي و صد درصدي. همبستگي مي تواند مثبت و يا منفي باشد.
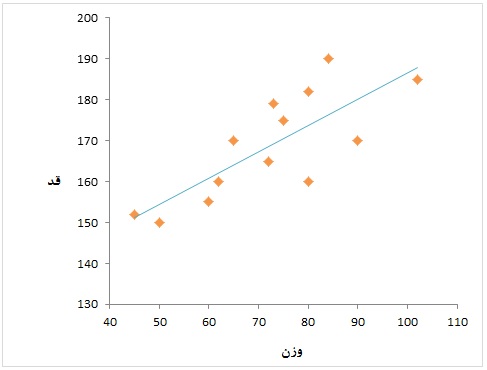
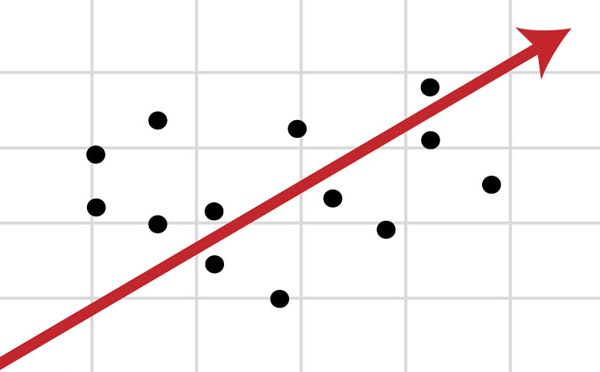
با رسم نمودار پراکنش که در اکسل نيز قابل ترسيم است، ميزان همبستگي دو متغير ديده مي شود.
نمودار پراکنش بين قد و وزن که داراي همبستگي مثبت مي باشند، به صورت زير است:
ضريب تعيين
ضريب تعيين معلوم مي کند که چند درصد از تغييرات متغير y ناشي از تغييرات متغير x است.
اگر ضريب همبستگي را به توان دو برسانيد، ضريب تعيين بدست خواهد آمد که باز هم عددي بين صفر و يک است. به عنوان مثال چنانچه ضريب تعيين عدد 0.65 بدست آيد، يعني با مي توانيم 65 درصد از تغييرات در متغير «وزن» را با تغييرات متغير «قد» بيان کنيم.
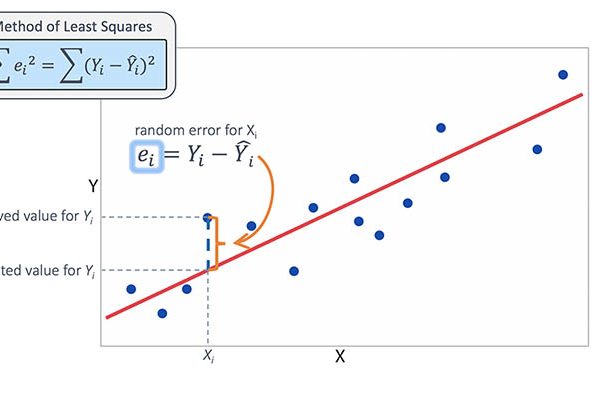
برازش خط رگرسيون y بر x
حال که تا حدودي با مفاهيم آشنا شديم، در اينجا عملا به محاسبه معادله رگرسيون و رگرسيون خطي y بر اساس x مي پردازيم. لازم است تعريف کنيم چنانچه بخواهيم متغير y را بر اساس متغير x پيش بيني و بيان کنيم، به متغير x متغير مستقل و به متغير y متغير وابسته مي گوييم.
براي محاسبه معادله رگرسيون خطي در اينجا لازم است به سراغ نرم افزاري آماري مانند اس پي اس اس يا SPSS برويم.
انواع رگرسيون
محقق گرامي؛ رگرسيوني که در اينجا به شرح آن پرداختيم، رگرسيون خطي ساده با دو متغير بود. رگرسيون حالات و انواع ديگري نيز دارد که به آن اشاره مي کنيم.
مي توان به جاي يک متغير وابسته (وزن) و يک متغير مستقل (قد)، يک متغير وابسته داشت و چندين متغير مستقل. يا اينکه به جاي رابطه خطي بين متغيرها، به دنبال کشف و بيان رابطه غير خطي باشيم.
برخي مواقع متغير وابسته فقط مقادير صفر يا يک را مي گيرد و يا اينکه متغيرها مقادير گسسته يا رتبه اي داشته باشند.
قبول سفارش تحلیل آماری فصل 4 پایان نامه با نرم افزار آماری
در صورتی که مایل بودید می توانید انجام تحلیل آماری فصل 4 پایان نامه خود و تجزیه و تحلیل نتایج پرسشنامه ها و آزمون فرضیات پایان نامه خود را به تیم تحلیلگران با تجربه اطمینان شرق بسپارید.
برای بررسی و اعلام قیمت و زمان انجام تحلیل، به ما واتساپ بزنید و مدل و فرضیات و پرسشنامه و اطلاعات لازم را ارسال نمایید.
براي مشاهده ساير مقاله هاي تحليل آماري اين وب سايت بر لينک زير کليک نماييد: صفحه مقاله هاي تحليل آماري



93 دیدگاه. همین الان خارج شوید
سلام رابطه بین خودراهبری یادگیری و عملکرد تحصیلی با کدوم ضریب همبستگی سنجیده میشود؟ پیرسون یا اسپیرمن. خودراهبری با پرسشنامه سنجیده میشود و عملکرد تحصیلی همان معدل هست. از طریق پیرسون سنجیده شده متاسفانه با ضریب منفی مواجه شده ایم. شاید روش اشتباه بوده. نظر من روی اسپیرمن است.
سلام؛ اینکه با کدام آزمون (پیرسون یا اسپیرمن) همبستگی آزمون شود بستگی به این دارد که تعداد داده های شما چند تا باشد و اینکه آیا داده ها دارای توزیع نرمال هستند یا خیر.
اگر داده های دو متغیر دارای توزیع نرمال باشند با همبستگی پیرسون آزمون می شود و گرنه با ضریب همبستگی اسپیرمن که آزاد توزیع است.
می توانید داده های خود را ارسال تا ما همبستگی را برای شما محاسبه (به روش اصولی و دقیق) و گزارش تحلیلی آنرا ارسال کنیم.
باسلام
اطلاعاتی در مورد LR statistics که اصلا چی هست و چه کاربردی دارد و آماره fو نحوه تفسیرش چه جوری هست میخواستم.
باتشکر
سلام؛ متوجه منظورتان از LR نشدم. مخفف چیست؟ آیا منظورتان رگرسیون لجستیک است؟
سلام ممنون از پیگیریتون
با عنوان نسبت درستنمایی ذکر شده ولی من کاراییشو واینکه نحوه تفسیرش چه جوریه رونمیدونم لطفا اماره fو اینکه تفسیرش چه جوری هست رو بگین
البته تفسیرشون از طریق سطح معنی داری رو بلدم از رو اماره بلد نیستم.
سلام؛ حقیقتش در خصوص نسبت درستنمایی در این موقعیت چیزی نمی توانم بگویم. اما روش حداکثر درستنمایی در آمار وجود دارد که یک روش برآورد آماره ها در کنار روش حداقل مجموع مربعات می باشد.
اما در جریان باشید که کلا تفسیر آماره ها از روی سطح معنی داری و مقایسه آن با 0.05 صورت می گیرد و از روی آماره تصمیم گیری کردن عملا خیلی سخت است.
سلام ممنون از مطالب خوبتون
من به دنبال اطلاعات در مورد ridge regression و نسخه کرنلی اون هستم ممنون میشم راهنمایی کنید
سلام؛ خواهش. متاسفانه در این زمینه نمی تونیم بهتون کمک کنیم.
باسلام برای توزیع نرمال یه مثال بیارید
سلام. در این آموزش ویدئویی چند رشته عددی با توزیع نرمال آمده ، همراه با آموزش نحوه بررسی نرمال بودن داده ها:
https://spss-iran.ir/product/normal-test/
سلام وقت بخیر من میخواستم بدونم در رگرسیون که با spss انجام میدیم چه کاری باید روی داده ها انجام داد تا درصد پیشبینی یا همون ضریب تعیین r2 یک متغیر روی متغیر دیگه رو بالا برد
سلام؛ حذف داده های پرت را امتحان کنید. ممکن است باعث افزایش ضریب تعیین شود
سلام خسته نباشید. سوالی که دارم این است که رگرسیون ساده و رگرسیون خطی و رگرسیون محلی اینها همه با هم یکی هستند برای یک متغییر مستقل و یک متغیر وابسته؟ اگر متفاوت هستند لطفا دیلی تفاوت را بیان کنید. یبسیار متشکرم
سلام؛ بله اگر فقط یک متغیر مستقل دارید و یک متغیر وابسته، اینها همه یکی هستند.
با سلام
من کارمند بازرگانی یک شرکت هستم دادههای زیادی در خصوص هزینه دریافت می کنم از قبیل هرینه روغن و ابزار و لوارم یدکی و ……
و هر ماه این هزینه را اعلام می کنم به مدیر عامل تا به حال فقط دادن اطلاعات بوده و هیچ تحلیل در ان نبوده به نظر شما من برای انجام تحلیل این موارد از کحا شروع کنم یا چه کتابی بخونم که بتوانم در این خصوص کارم را خوب انجام دهم
ضمنا من برای تامین کنندکان نیز فرمی داریم که باید هر سه ماه آنها را ارزیابی کنیم این ارزیابی بر اساس نمره هست آیا می شود ار علم آمار این مورد را نیز انجام داد.
با تشکر
سلام. یکی از آرزوهای من همین است که علم آمار در تمام بخشهای کشور ساری و جاری شود. همین که شما داده ها را ذخیره و ثبت می کنید خوب است و اینکه تصمیم بگیرید از این اطلاعات به نکات مدیریتی در راستای افزایش بهره وری برسید (با استفاده از علم آمار) بسیار بسیار خوب است.
کاری که باید بکنید این است که اطلاعات تان را به صورت منظم در یک فایل اکسل ذخیره و تجمیع کنید. این تحلیلها را می توانید داشته باشید:
1- ترسیم نمودار سری زمانی داده هایتان، مثلا سری زمانی هزینه های لوازم یدکی طی سه سال اخیر به تفکیک ماه.
2- مقایسه هزینه های هر سال با مدت مشابه سال گذشته- در کنار آن اگر درآمد را نیز مقایسه کنید کار زیبایی خواهد شد
3- بررسی و محاسبه تاثیر عوامل مختلف بر افزایش یا کاهش هزینه. مثلا تاثیر گرانی ارز بر هزینه ها
در خصوص تامین کنندگان نیز رتبه بندی آنها بسیار فکر خوبی است. با طراحی یک فرم از عملکرد تامین کنندگان و تبدیل کیفیت کارشان به داده های کمی (از طریق طیف 5 تایی لیکرت) و بعد میانگین گیری از امتیازات طیف لیکرت، می توانید بهترین تامین کنندگان خود را شناسایی و تشویق کنید و با بدترین ها خداحافظی نموده و جایگزین جدید پیدا کنید.
توجه شود که همه این کارها در محدوده آمار توصیفی است و نیازی به آزمون های آماری نیست. و همه این کارها با اکسل شدنی است
با سلام آيا رگرسيون و همبستگي در مواردي هم پوشاني دارند؟/ تشكر
سلام. بله ارتباط زیاد و شباهت هایی با هم دارند.
اگر دو متغیر با هم همبستگی بالایی داشته باشند، رگرسیون شان نیز معنی دار خواهد بود.
اما در مجموع دو آزمون آماری جداگانه با کاربردهای متفاوت هستند. رگرسیون کاملتر از همبستگی است و رابطه چندین متغیر مستقل با متغیر وابسته را می سنجد.
سلام
فرق بین ضریب همبستگی پیرسون و همستگی رگرسیون چیست؟ میتوانیم با یک مثال واضح بسازیم؟
سلام. در رگرسیون 2 یا بیشتر از 2 متغیر داریم و مایلیم تاثیر چند متغیر را بر روی یک متغیر (متغیر وابسته) بسنجیم.
اما در همبستگی ها فقط دو متغیر داریم که می خواهیم میزان همبستگی این دو را بسنجیم.
از منو “آموزش تحلیل آماری” مبحث رگرسیون را انتخاب و مقالاتش را ببینید. یا در سایت سرچ کنین تا مقالات بیشتری ببینید.
با سلام و وقت بخیر. در صورتی که یک متغیر مستقل و چند متغیر وابسته داشته باشیم، چطور باید رگرسیون رو انجام بدیم؟
سلام. چند بار رگرسیون را با متغیرهای وابسته مختلف انجام دهید
در این صورت نتیجه هر رگرسیون با نتیجه پیرسون یکسان خواهد بود؟
سلام. نتایج رگرسیون ها با نتایج همبستگی دو به دو با ضریب همبستگی پیرسون، متفاوت خواهند بود.
به نظرتون راه دیگه ای نیست. مثلا استفاده از Amos برای معادله ساختاری و تحلیل مسیر؟
قطعا این راه نیز هست. در ابتدا برای اینکه باعث سردرگمی شما نشود این نکته را نگفتم.
و گرنه در وضعیتی که شما دارید بهتر است از مدلسازی معادلات ساختاری استفاده کنید. وب سایت دیگر ما را ببینید که در زمینه تحلیل با لیزرل و ایموس است: http://www.lisrel.ir
از راهنماییتون خیلی متشکرم.
با سلام براتون مقدور هست که اثبات ریاضی ضرایب رگرسیون ۳متغیره رو برام ارسال بفرمایید۰با تشکر
سلام. نه متاسفانه. در این زمینه به کتابهای آماری مراجعه نمایید.
با سلام.ممنون از زحماتی که میکشید.ببخشید اطلاعاتی درباره رگرسیون وزنی میخواستم میشه راهنمایی بفرمائید .ممنون
سلام. متاسفانه مطلبی در این خصوص نداریم.
سلام، میشه معلومات بیشتری در مورد برازش رگرسیون بدید، مخصوصاً برازش به چه معنی
سلام. رگرسیون مبحث بسیار مفصلی در آمار است.
برازش به معنی برازندگی است. مثلا شما وقتی یک لباس انتخاب می کنید، وقتی این لباس برازنده شماست که تنگ، گشاد، کوتاه یا بلند نباشد. مدل رگرسیون هم همینطوری است.
وقتی یک مدل رگرسیون بر داده ها برازش دارد یا فیت است که به خوبی داده ها و متغیرها را تبیین کند و روابط بین آنها را توضیح دهد. یعنی بتواند روابط را در قالب فرمول ریاضی وار رگرسیون نمایش دهد.
وقتی روابط بین متغیرها فرموله شود آنگاه می توان به اثبات یا رد فرضیات تحقیق پرداخت
سلام
من میخوام اثر جنسیت ک متغیر کیفی هست روی حافظه بررسی کنم که کمی هست. فک می کنم باید مقایسه کنم یعنی از t-test استفاده کنم اما برای مقاله ازم خواستن رگرسیون بگیرم. مگر رگرسیون بین دو مقدار کمی نباید انجام بشه؟
سلام. بله رگرسیون بین دو مقدار کمی تعریف می شود.
اما مدلی از رگرسیون داریم که متغیر وابسته آن صفر و یک و کیفی است به نام رگرسیون پروبیت یا لوجیت. شاید منظورشان این نوع رگرسیون بوده و متغیر جنسیت به عنوان متغیر وابسته آن تعریف گردد.
ممنون
پس اگر جنسیت متغیر مستقل من باشه نباید رگرسیون انجام بدم؟
سلام. توجه شود که امکان دارد که متغیر مستقل نیز به صورت کیفی باشد که در اقتصاد سنجی به آن متغیر مجازی یا دامی می گویند.
اما در خصوص کار شما، اگر فقط همین دو متغیر را دارید و متغیر مستقل کیفی است، رگرسیون درستی نیست (حداقل ما تا بحال نداشته ایم این حالت را). مگر اینکه متغیرهای دیگری هم داشته باشید و رگرسیون شما با مثلا با 5 متغیر انجام شود و یکیش مستقل باشد.
خیلییی ممنونم???
با سلام
اگر بخوایم دو گروه رو از لحاظ ویژگی های فیزیولوژیکی با هم مقایسه کنید از چه روش تحقیق و چه تست های آماری باید استفاده کنیم؟ تست تی مستقل فقط؟
سلام. تی تست هست. از رگرسیون هم می توانید استفاده نمایید (اگر داده ها دارای توزیع نرمال باشند). ولی در اصل روش تحقیق شما و نوع نگارش فرضیات است که تعیین می کند بهترین آزمون آماری کدام است. می توانید با همکاران ما ارتباط و مشاوره بگیرید.
با سلام
آیا امکان دارد نحوه ی ارائه نتایج جواب حاصل از رگرسیون بین دو متغیر قد و وزن را بین کنید
ممنون
سلام. اگر منظورتان نحوه خروجی گرفتن است که خودش یک آموزش جداگانه نیاز دارد. و اگر منظورتان نحوه تحلیل خروجی رگرسیون است، این صفحه سایت را ببینید:
آزمون معنی داری رگرسیون و تحلیل خروجی spss
ممنون از لطف شما.موفق باشید
سلام من پایان نامم یک قسمتش مربوط به رگرسیون خطی ساده هست .میتونم فایلشو بفرستم در عرض دو روز رگرسونو برام تحلیل کنین.خواهشا هزینش کم باشه .منم دانشجو هستم.ممنون میشم از لطفتون
سلام. احتمالا همین مبحث رگرسیون اساس فصل 4 شما خواهد بود. زیرا در فصل 4 نتایج تجزیه و تحلیل داده ها و مشاهدات ارائه می گردد.
داده ها و فرضیات و مدل رگرسیون خود را برای همکاران ما ارسال نمایید تا قیمت و زمان به شما اعلام نمایند. انجام این تحلیل معمولا حدود 4 یا 5 روز زمان می برد. از نظر هزینه نیز این شرکت قیمت هایی مناسب و متناسب با کار انجام شده دارد.
سلام میشه لطفا بگین رگرسیون محلی چیه، سپاس.
سلام. نمیدانم منظورتان چیست
سلام، من به روشی نیاز دارم تا ارتباط بین یک بردار از داده را با بردار خروجی پیدا کنم.
در حقیقت بعد از استخراج یک ویژگی از 100 تصویر من یک بردار 100*1 دارم و بردار خروجی من هم شامل 100 عدد است که برچسب هر تصویر را نشان میدهد.
من به روشی نیاز دارم تا ویژگی هایی که استخراج کردم رو به برچسب های تصویر که در بردار خروجی قرار داره رابطه اونها رو پیدا کنه…
فقط اسم روش یا روش ها هم برام کافیه…
ممنون از شما…
سلام. سوال سختی است. با کمک رگرسیون شما می توانید ارتباط چند متغیر مستقل (بردار) را با یک متغیر خاص (متغیر یا بردار وابسته) پیدا کنید و اثر گذاری متغیرهای مستقل بر روی متغیر وابسته را آزمون کنید. اما در مورد شما نمیدانم این روش کارایی دارد یا خیر و آیا شما به دنبال بررسی اثر گذاری هستید یا خیر.
با سلام و سپاس از سایت خوبتون
من دانشجو هستم و علاقمندم به مباحث آماری. مدتی با spss کار میکردم؛ ولی به نظرم چندان جذاب نبود. بعضی از دوستان میگن که R هم همه ی قابلیت های spss رو داره و در عوض، رایگان هست. می خواستم بدونم آیا واقعاً هر کاری که در spss میشه انجام داد رو با R هم میشه انجام داد؟
خیلی ممنونم
سلام. فقط اگر رشته شما آمار است توصیه می کنم R را هم یاد بگیرید.
نرم افزار آر بسیار قوی است و همه مطالب را در بر می گیرد. اپن سورس هم هست و دست شما بسیار باز است در کار با این نرم افزار.
منتها به شدت تخصصی است و منو ندارد و به صورت کد نویسی است.
ممنون
سلام ممنون از کمک شما .لطفا quadratic trend را به زبان ساده توضیح دهید سپاسگزارم
سلام
من برای محاسبه اهمیت یک سری از ابعاد تحقیقم نیاز به محاسبه نمره عاملی دارم. اما متاسفانه توزیع داده هام نرمال نیست. باید چه کار کنم داده ها را نرمال کنم یا برای نمره عاملی معادل ناپارامتریک داره؟
ممنون می شم راهنمایی بفرمایید
سلام.سوال شما نامفهوم است.
اگر منظورتون بارعاملي در مدل مي باشد. بايد از نرم افزار معادلات ساختاري استفاده کنيد. اگر داده ها نرمال نيستند مي توان از اسمارت پي ال اس استفاده کرد
سلام خسته نباشید. در جدولی از یافته های من به نام parameter estimates ستونی با عنوان B امده. ایا این مقدارهمان ضریب رگرسیون است
سلام. بله
اگر بین دو متغییر ارتباط منفی باشد)negative relationship) در بررسی multiple regressionبه این معنی است که یکی از متغییر negative predictor ؟
لزوما اینگونه نیست. زیرا در رگرسیون چندگانه ممکن است ضریب آن متغیر مد نظر معنی دار نباشد، اما در همبستگی دو به دو معنی دار و منفی باشد.
چه جوری میشه فهمید که یک متغییر predictor متغییر دیگه هست؟
بر اساس مبانی نظری و هدف شما از انجام تحلیل. یا بر اساس مدل رگرسیونی از قبل تعیین شده در منابع علمی.
البته آزمون علیت نیز در این زمینه کاربرد دارد.
با سلام و احترام، من دانشجوی کارشناسی ارشد در رشته جی آی اس هستم و موضوع پایان نامه من در مورد مدل سازی بیماری آنفلوآنزای فوق حاد پرندگان در استان گیلان هست. در این خصوص 17 متغیر در نظر گرفته شده اند که با استفاده از روش رگرسیون تقویت شده(Boosted Regresion Tree) برای هرکدام از متغیر ها وزن و انحراف معیار محاسبه شده است، سوال بنده این است که آیا وزن این متغیر ها همان ضریب همبستگی بین متغیر وابسته و متغیر مستقل است و همچنین انحراف معیار محاسبه شده چه مفهومی را بیان می کند.
بسیار ممنون خواهم شد اگر راهنمائی بفرمائید.
سلام. نه. در رگرسیون نمی شود گفت که ضریب برآورد شده متغیرها در مدل رگرسیون، همان ضریب همبستگی بین متغیر وابسته و مستقل است.
سلام.
هر چه مقدار همبستگي به عدد يک نزديک تر باشد، همبستگي بين دو متغير بيشتر است و هر چه به صفر نزديک تر باشد، همبستگي بالاتر خواهد بود.
این جمله یه اشتباهی نداره؟
سلام. ممنون از دقت نظر شما. اصلاح شد:
هر چه مقدار همبستگي به عدد يک نزديک تر باشد، همبستگي بين دو متغير بيشتر است و هر چه به صفر نزديک تر باشد، همبستگي کمتر خواهد بود.
سلام لطفا در خصوص سه جدول تحلیل رگرسیون خطی در spss کمی توضیح دهید.ممنون
سلام وقت بخیر
سوال بنده در خصوص محاسبه “درصد رشد” متغیر وابسته می باشد.
بعنوان مثال در یک مرغ داری روزانه مقادیری دانه به مرغها داده می شود و این مقدار عنوان متغیر مستقل بصورت روزانه ثبت می گردد و تغییرات وزن مرغها نیز بعنوان متغیر وابسته ثبت می شود.
سوال بنده این است آیا اصولا ثبت درصد رشد وزن مرغها مثلا 5 روز پس از خوردن N گرم دانه می تواند بعنوان متغیر وابسته مورد محاسبه قرار گیرد و نه مقدار وزن مرغ ها ؟
فرضا در روز N یکصد گرم دانه به مرغ داده می شود و در روز N+5 دو درصد نسبت به روز N افزایش وزن داشته ایم .
باکمال تشکر
سلام. بله شما با توجه به تعریفی که از متغیر وابسته دارید می توانید آنرا محاسبه کنید و در رگرسیون بیاورید.
منتها توجه به : مبانی نظری، مقالات معتبر مشابه، قابلیت اندازه گیری بهتر، قابلیت نتیجه گیری بهتر، نوع فرضیاتی که قصد آزمون دارید، همه از مواردی است که به شما کمک می کند متغیر وابسته خود را تعریف کنید.
باسلام و احترام
دوست عزیز بنده مقاله ای کار کرده ام که واقعیتش خیلی در مورد این مقاله زحمت کشیدم و برای دفاع از پایان نامم به پذیرشش نیاز شدید دارم، از طرفی مقاله بنده الان اصلاح خورده و با روش رگرسیون گام به گام کار کردم. منتهی داور این سه مورد را تأکیدا خواسته که ضمن مقاله بهشون اشاره کنم، اما من خیلی از این سه مورد سر در نیاوردم. برای همین خواهش می کنم که لطفا در مورد این سه مورد ذیل در رگرسیون گام به گام توضیح بدین.
1- معیارهای برازندگی مدل کمی
2- باقی مانده نتایج مدل کمی
3- میزان تحقق پذیری نتایج
ممنونم ازتون
سلام. در اصل داور از شما خواسته پیش فرضهایی که یک رگرسیون می بایست داشته باشد + شاخص های نیکویی برازش را در گزارش خود بیاورید.
1 و 2: نرمال بودن باقیمانده ها، برابر صفر بودن میانگین باقیمانده ها، ثابت بودن واریانس باقیمانده ها را بررسی کنید.
3: ضریب تعیین را گزارش کنید
با عرض سلام وخسته نباشید .
خواهشمند است اگر بی ادبی نیست مرجعی در زمینه Compare the methods of fuzzy regression model by ( Tanaka’s ,,,,savic and perdycz ,,,,,Diamond ) methodes with application
معرفی نمایید در این زمینه دوست دارم که مطالعه نماییم . با تشکر فراوان . سپاس
سلام. متاسفانه منبعی سراغ نداریم.
بازدید کنندگان محترم اگر سراغ دارند لطفا در پاسخ به همین دیدگاه درج کنند
سلام
تشکر فراوان
سپاس
سلام خسته نباشید برای برازش یک رگرسیون غیرخطی چندجمله ای درجه دوم به یک متغیر وابسته و 2 متغیر مستقل مدلم رو باید چجوری بنویسم؟
سلام
نیاز به برنامه نویسی با نرم افزاری آماری مثل R هست
سلام لطفا در خصوص آزمونهای پیش فرض رگرسیون چند متغیره مطالبی رو به اشتراک بگذارید.
سلام خسته نباشید سوال من این هستش که چرا در یک مدل مبتنی بر داده (مثل مدل رگرسیون یا حتی شبکه عصبی)وقتی تعداد پارامترهای مدل با تعداد داده های آموزشی برابر باشد (یا حتی بیشتر باشد)می تواند تمام خروجی های مدل برای داده های آموزشی بدون خطا باشد؟
سلام. شبکه های عصبی را اطلاع ندارم اما در رگرسیون، حتما و حتما بایستی تعداد داده ها، چندین برابر تعداد پارامترها و متغیرهای مدل باشد. اگر مساوی باشند اصلا اعتبار ندارد این مدل و چه بسا نرم افزار خروجی تولید نکند.
با سلام. من بر روی دادههای دمای محور و چرخهای قطارها توسط سنسور گرمایی کار میکنم. حجم دادهها خیلی زیاد است. از من خواسته شده دقت این سنسورها رو با توجه به دادهی از گذشته تا کنون در سراسر کشور برسی کنم. و در آینده توسط این دادها به بررسی معایب خود قطارها بپردازم. و حتا اگر بشود پیشبینی کنم تا از بروز حادثه جلوگیری شود. نرم افزار من ثث هست. نمیدانام چطور میشود با استفاده از معادلات امر این کار را انجام داد. میتوانید پیشنهادی به من بدهید؟ خیلی سپاسگزار میشوم. نکته این است ک عوامل بسیار زیادی بر روی دمای چرخها و محورهای قطار تاثیر دارد. مثل سرعت، ترمز ناگهانی، پیچ ریل، دمای محیط و…
سلام خسته نباشید میشه قضیه های گازمارکوف را به طور خلاصه واضیح سازید
عمل رگرسیون در جی ای اس هم صورت میگیرد یا نه؟ آیا رگرسیون نوعی درونیابی هست ینی مانند کریجینگ و … عمل میکند؟ کلا توضیحی در رابطه با رگرسیون
در خصوص نرم افزار GIS نمیدانم که آیا رگرسیون هم دارد یا خیر.
رگرسیون به معنای بازگشت است و می آید با توجه به سابقه قبلی ارتباط و همگرایی چند متغیر با هم، رابطه ای ریاضی گونه برای این ارتباط تولید می کند. بگونه ای که با جایگذاری اعداد برای متغیرهای مستقل می شود عدد متغیر وابسته را با احتمالی مشخص برآورد کرد.
سلام ووقت بخیر برای انتخاب یک مدل در اقتصاد ایران که دارای 4 متغیر باشد راهنمایی میخواستم باتشکر
سلام. می بایست مطابق با مقالات معتبر در مجله های علمی معتبر اقدام نمایید. با استاد مشورت داشته باشید.
سلام
وقت بخیر
من میخوام ازتون مشاوره بگیرم … لطفا هزینه مشاوره و راه ارتباطی رو بهم اطلاع میدین..
ممنونم
سلام. در خصوص مشاوره، مشاوره تلفنی وجود دارد. اما دقت داشته باشید که این شیوه مشاوره نیاز به عوامل زیادی برای موفقیت دارد. مثل اینکه موضوع کاملا مشخص باشد و واقعا بتوان مساله را به صورت تلفنی و یا در واتساپ انتقال داد.
مثلا آموزش نرم افزار را نمی شود در مشاوره تلفنی گفت.
بهرحال حتما قبل از واریز وجه مشاوره، در واتساپ به شماره9198180991 طرح موضوع داشته باشید و این وجه به دلیل وقتی که همکاران ما می گذارند، اصلا قابل برگشت نیست. نحوه خریداری بسته آموزش تلفنی:
https://www.spss-iran.com/product/consultant/
منظور از رگرسیون پارامتری که برای تحلیل بقا استفاده میشه چیه؟
سلام، آیا اگه ضریب تعیین مون زیاد شده مثلا R^2= 0.81
میشه ضریب خط رگرسیون کم باشه، مثلا 0.01، ازوما نباید این دو تا تو یه چهت باشن؟
سلام. نه. این دو ارتباط خاصی به هم ندارن.
معنی داری ضریب رگرسیون مهم است نه مقدار آن.
سلام ببخشید اگر در یک مطالعه متغیر وابسته ی ما شامل مقادیر پیوسته باشد مانند بروز یک بیماری، آیا رگرسیون مناسب OLS است یا پواسون؟ سپاسگزارم
سلام. رگرسیون معمولی یا OLS مناسب است.
با سلام ،
برای تحلیل یک طرح در رشته پزشکی آنالیز طبقه ای و شاخص اثر مربوطه و انالیز رگرسیون لجستیک انجام گردید. در نتایج آنالیز رگرسیون، اعلام گردید متغیرهای کلسترول و UA معنی دار بودند. در متن مقاله این تحلیل چونه عنوان گردد؟
سلام. بنویسید
با توجه به نتایج آزمون رگرسیون، و اینکه ضریب معنی داری (PValue) متغیرهای کلسترول و UA کمتر از 0.05 می باشد، نتیجه می گیریم که این دو متغیر معنی دار می باشند. این نشان می دهد که این متغیرها اثر معنی داری بر روی متغیر وابسته دارند.
البته قبلش باید معنی داری مدل رگرسیون به صورت کلی و آماره اف آن را نیز تحلیل نمایید. خلاصه جزئیات زیاد دارد.
اگر خواستید، می توانید انجام تحلیل رگرسیون خود را به همکاران ما در «اطمینان شرق» بسپارید تا انجام دهند.