1- نمونه گیری سیستماتیک چطور انجام می گردد؟

ایده ی اساسی نمونه گیری سیستماتیک انتخاب منظم تعدادی از افراد موجود در یک لیست می باشد.

فرض کنید قرار است نمونه ای از  اسم از فهرستی طولانی انتخاب شود.یک روش ساده برای این کار آن است که فاصله ای مناسب برگزیده و اسامی را در فواصل مساوی در طول فهرست انتخاب کنیم. اگر نقطه ی شروع برای این روند منظم انتخاب ، تصادفی باشد نتیجه یک نمونه گیری سیستماتیک است.

به این ترتیب نمونه ای که به وسیله ی انتخاب یک عضو از بین اولین عضو یک فهرست ، سپس انتخاب هر k مین عضو بعد از آن حاصل شود، یک نمونه تصادفی سیستماتیک 1 در K با شروع تصادفی نامیده می شود.

اجرای روش نمونه گیری سیستماتیک اغلب آسان تر از تصادفی ساده است و همچنین امکان بروز خطا از طرف پرسشگر کاهش می یابد. برای مثال با استفاده از نمونه گیری تصادفی انتخاب نمونه به حجم  n از خریداران واقع در بخشی از یک خیابان ، پرسشگر نمی تواند تعیین کند که کدام خریدار را در نمونه قرار دهد زیرا تا زمانی که تمام خریدارن از آن قسمت عبور نکرده اند اندازه ی جمعیت معلوم نیست. در مقابل پرسشگر می تواند یک نمونه ی سیستماتیک (مثلاً 1در 20) را تا رسیدن به حجم نمونه ی مورد نظر اختیار کند.

 علاوه بر آنچه گغته شد، نمونه گیری سیستماتیک اغلب اطلاعات بیشتری به ازای هزینه ی هر واحد از نمونه گیری تصادفی ساده ارائه می دهد. یک نمونه ی سیستماتیک به طور کلّی به صورت یکنواخت تر روی کلیه ی جمعیت توزیع می شود و در نتیجه اطلاعات بیشتری درباره ی جامعه از یک جامعه نسبت به نمونه گیری تصادفی ساده با همان حجم بدست می دهد.

برای مثال فرض کنید برای تعیین درصد پرونده هایی که نادرست بایگانی شده اند ، می خواهیم از بین 1000 پرونده نمونه ای به حجم 200 تهیه کنیم. حال اگر بدانیم 500 پرونده ی اول درست بوده و بعد به دلیل تغییر کارمند امکان اشتباه در پرونده های بعدی وجود دارد، استفاده از نمونه گیری تصادفی ساده مناسب نیست زیرا ممکن است تمام نمونه ها از پرونده های گروه اول یا دوم انتخاب شوند. در حالیکه نمونه گیری سیستماتیک تعداد مساوی از هر دو گروه را انتخاب می کند. مثال های مختلفی برای استفاده از این نوع نمونه گیری وجود دارد مانند طرح های کنترل کیفیت صنعتی ، طرح های نظرسنجی از جمعیت های در حال حرکت و یا در نمونه گیری از کرت های مربوط به کشاورزی و … .

2- برآورد میانگین و مقدار کل جامعه

 از آنجاییکه هدف اغلب بررسی های نمونه ای برآورد یک یا چند پارامتر جامعه است. میانگین جامعه در نمونه گیری سیستماتیک به کمک میانگین نمونه برآورد می شود.

 برآورد میانگین جامعه :                           

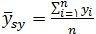
واریانس برآوردگر میانگین جامعه به صورت :             

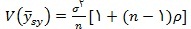
تعریف می شود که به  ρ ، ضریب همبستگی بین ازواج درون نمونه ی سیستماتیک ، بستگی دارد. اگر ρ  به  1 نزدیک باشد ، اعضای درون نمونه نسبت به خصیصه ای که اندازه گیری می شود کاملا مشابه اند. و نمونه ی سیستماتیک واریانس بزرگی نسبت به نمونه گیری تصادفی ساده دارد. اگر ρ منفی باشد یعنی اعضای درون یک نمونه کاملا متفاوت باشند ، نمونه گیری سیستماتیک ممکن است بهتر از تصادفی ساده باشد. برای ρ های نزدیک به صفر و N نسبتاً بزرگ این دو روش نمونه گیری تقریبا معادل اند.

3- نمونه گیری سیستماتیک در جوامع مختلف

در نمونه گیری سیستماتیک توجه به نوع قرار گرفتن اعضا در جامعه دارای اهمیت است. سه نوع جامعه ی مختلف را می توان در نظر گرفت ، جامعه تصادفی ، جامعه مرتّب شده و جامعه متناوب.

1-3- جامعه تصادفی

جامعه ای تصادفی است که اعضای آن دارای ترتیب خاصی نبوده و به صورت تصادفی قرار گرفته باشند. در نمونه ی سیستماتیک که از یک جامعه ی تصادفی انتخاب می شود انتظار می رود اعضای نمونه متجانس بوده و بنابراین مقدار ρ صفر باشد. بنابراین زمانی که N بزرگ است واریانس y̅_sy تقریباً معادل واریانس y̅ بر اساس یک نمونه تصادفی ساده است. در این حالت نمونه گیری سیستماتیک و تصادفی ساده معادل اند.

برای مثال یک پژوهشگر علاقمند است متوسط اقلام دارویی که توسط پزشکان معین در طول سال گذشته تجویز شده است ، تعیین نماید. اگر چارچوب شامل فهرست الفبایی از پزشکان باشد، این فرض که اسامی فهرست به تعداد اقلام دارویی وابسته نیست قابل قبول است (0=ρ) و بنابراین نمونه گیری سیستماتیک و تصادفی ساده معادل اند.

2-3- جامعه مرتب شده

جامعه ای مرتب است که اعضای آن نسبت به یک روش از نظر بزرگی مرتّب شده باشند.

یک نمونه ی سیستماتیک برگرفته از جامعه ای مرتب به طور کلّی نامتجانس با ρ<=0 است .ثابت می شود که هرگاه N بزرگ و ρ<=0  باشد

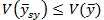
 است . بنابراین در یک جامعه ی مرتب یک نمونه ی سیستماتیک به ازای هر واحد هزینه اطلاعات بیشتری از نمونه گیری تصادفی ساده می دهد.

از آنجایی که ما نمی توانیم یک برآورد نااریب از نمونه ارائه دهیم یک برآورد نسبتاً خوب که البته بزرگتر از مقدار مورد انتظار است برای

 V(y̅_sy)  عبارت است از :

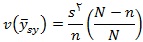
 به عنوان یک مثال در این زمینه ، فرض کنید برای برآورد اثربخشی آموزش در یک کلاس درس عمومی از دانشجویان برای ارزیابی مدرّس براساس یک مقیاس عدی سوال می شود و یک نمونه از فهرست ارزیابی ها که از نظر عددی به صورت صعود ی مرتب شده است گرفته می شود. جامعه ی اندازه گیریهایی که نمونه از آن استخراج شده است به عنوان جامعه ی مرتب شده در نظر گرفته می شود.

3-3- جامعه ی تناوبی

جامعه ای تناوبی است که اعضای آن تغییرات دوره ای داشته باشند.

برای مثال فرض کنید می خواهیم متوسط فروش روزانه ی خواروبار را در یک فروشگاه زنجیره ای محاسبه کنیم. از آنجایی که معمولاً حداکثر فروش در آخر هفته می باشد ، جامعه ی مورد نظر تناوبی است. موثر بودن یک نمونه ی 1 در k بستگی به مقداری دارد که برای k انتخاب می کنیم. اگر ما فروش روزانه را هر چهارشنبه بررسی کنیم احتمالا میانگین جامعه را کم برآورد خواهیم کرد. و یا اگر هر جمعه نمونه گیری کنیم، برآورد مورد نظر بیش از حد واقعی خواهد بود. در چنین حالتی می توان نمونه گیری را مثلا هر 9 روز یک بار انجام داد. به این ترتیب از تمام روزها با فروش زیاد و کم نمونه گیری به عمل خواهد آمد.

 اعضای یک نمونه ی سیستماتیک که از جامعه ی تناوبی به دست آمده است می تواند متجانس باشد  . در این حالت نیز ثابت می شود اگر N بزرگ باشد و ρ>0  آن گاه :   

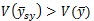
بنابراین نمونه گیری سیستماتیک به ازای هر واحد هزینه ، اطلاعات کمتری از نمونه ی تصادفی ساده فراهم می آورد. از آنجایی که واریانس نمونه گیری سیستماتیک در این حالت نیز قابل محاسبه نمی باشد ، این واریانس به کمک

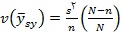
 برآورد می شود که البته این برآوردگر مقداری کمتر از مقدار واقعی را برآورد می کند.

 برای جلوگیری از این مشکل که با نمونه گیری از جامعه تناوبی بوجود می آید ، پژوهشگر باید نقطه ی شروع تصادفی را چندین بار تغییر دهد. این روش احتمال انتخاب مشاهدات از موقعیت نسبی یکسان را کاهش می دهد. روش انتخاب چند نقطه ی شروع تصادفی در طول نمونه ی سیستماتیک ، اثر به هم ریختن اعضای جامعه و سپس انتخاب یک نمونه ی سیستماتیک را دارد.

4- انتخاب حجم نمونه

 برای بدست آوردن تعداد مشاهدات لازم برای برآورد میانگین جامعه با حداکثر خطای  B از رابطه ی زیر

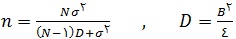
استفاده می کنیم. که در آن

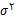
  با استفاده از اطلاعاتی که از تحقیقات مشابه پیشین بدست آمده و یا به کمک یک نمونه ی اولیه قابل محاسبه است.

منبع : مقدمه ای بربررسی های نمونه ای . نوشته ی شیفر و مندنهال. ترجمه ی دکتر ارقامی ، دکتر بزرگنیا و دکتر سنجری . انتشارات دانشگاه فردوسی مشهد.