تعريف پايايي
پایایی، همسانی نمره های افراد برای یک مجموعه از آیتم ها در دو موقعیت جداگانه یا در دو ابزار هم ارز را نشان می دهد. معمولاً از روش های همسانی درونی، دو نیمه کردن، آزمون-بازآزمون و پایایی درون رده ای برای اندازه گیری آن استفاده می شود.
پایایی یک ابزار به افراد تشکیل دهنده ی جامعه آماری مورد نظر بستگی دارد ، به طوری که اگر افراد یک جامعه شناخت بهتری از ابزار مورد نظر داشته باشند، پایایی آن ابزار در این جامعه بالاتر است. بنابراین نیاز است که پایایی (روایی) یک ابزار در جامعه ای که هدف مطالعه است ، ارزیابی گردد.
1- ارزیابی پایایی با روش همسانی درونی (آلفای کرونباخ)
این روش برآوردی از میزان همبستگی میان متغیرهایی که سازه یا مقیاس مورد نظر را می سازند، بدست می دهد. شاخص متداول برای ارزیابی پایایی در این روش، ضریب آلفای کرونباخ می باشد. مقدار صفر این شاخص عدم پایایی مقیاس مورد نظر را نشان می دهد. در مقابل مقدار عددی 1 برای این شاخص بیانگر پایایی کامل مقیاس مورد نظر است.
فرمول محاسباتی آلفای کرونباخ به صورت زیر است :
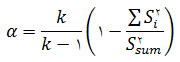
که در آن S_i^2 واریانس سؤال i ام و S_sum^2 واریانس مجموع سؤالات است. بنابراین α به تعداد سؤالات و میزان همبستگی بین آن ها بستگی دارد. اگر امتیاز واقعی به سؤالات داده نشود و پاسخ های افراد کاملاً به یکدیگر بی ارتباط باشد α به سمت صفر میل میکند. اگر تمام سؤالات قابل اعتماد باشند و یک نتیجه را نشان دهند، این ضریب 1 خواهد بود.
در ارتباط با آلفای کرونباخ نکات زیر حائز اهمیت است :
1-1) نقطه برش های متداول برای تفسیر آلفا
در ارتباط با حد مطلوب آلفای کرونباخ نظرات متفاوتی بیان می شود. بلند وآلتمن (1997) معتقد هستند که مقیاس هایی که برای ارزیابی های بالینی به کار می روند بایستی در مقایسه با مقیاس های مورد استفاده در پژوهش های غیر بالینی دارای پایایی بیشتری باشند. بر این اساس آن ها ضریب آلفای بین 0.7 و 0.8 را برای مقاصد پژوهشی پیشنهاد می کنند ولی در مقاصد بالینی مقدار آلفای مقیاس های مورد بررسی باید بزرگتر از 0.9 باشد.
2-1) تعداد آیتمهای تشکیل دهنده ی یک مقیاس
با توجه به تفسیری که برای α بیان شد، مقدار ضریب آلفای کرونباخ یک مقیاس با افزایش تعداد آیتم های آن مقیاس افزایش می یابد. بنابراین افزایش تعداد آیتم های یک مقیاس راهی برای سوق دادن ضریب آلفا به سمت یک مقدارقابل قبول برای مقیاس است. همچنین می توان نتیجه گرفت که مقیاس های با تعداد آیتم بیشتر پایاتر از مقیاس ها با تعداد آیتم های کمتر هستند.
علاوه براین مقایسه ضریب آلفا دو مقیاس با تعداد آیتم های نابرابر مناسب نیست. همچنین هنگامی که تعداد آیتم های یک مقیاس محدود است، پیشنهاد می شود به میانگین همبستگی درونی آیتم ها نیز توجه شود، براساس توصیه کاکس و فرگوسن(1994) ، مقیاسی قابل قبول است که میانگین همبستگی درونی آیتم های آن بین 0.2 تا 0.4 باشد.
3-1) استفاده از آلفا برای حذف آیتم های نامناسب
در صورتی که برآوردی از مقدار آلفا با حذف یک آیتم خاص بهبود یابد، این شاخص راهی برای حذف آیتم های ناهمگون با سایر آیتم های تشکیل دهنده ی یک مقیاس، فراهم می آورد. علاوه بر این همبستگی ضعیف بین آیتم و کل مقیاس، نشان دهنده ی آیتمی است که می تواند کاندیدای حذف باشد. همچنین همبستگی منفی یک آیتم با کل مقیاس حاکی از آن است که آیتم مورد نظر باید به صورت معکوس کدگذاری شود.
{اینکه چطور با استفاده از آلفای کرونباخ، سوال نامناسب را در پرسشنامه خود بیابید و آنرا حذف کنید در این آموزش ویدئویی بیان شده است: آموزش ویدئویی محاسبه آلفای کرونباخ با spss و اکسل}
2- ارزیابی پایایی با روش دو نیمه کردن
در این روش میزانی از همسانی دو مجموعه از آیتم ها که هدف واحدی را اندازه گیری می کنند، ارزیابی می شود ،برای محاسبه پایایی با این روش از دو شاخص ضریب پایایی دو نیمه کردن اسپیرمن-براون و یا گاتمن استفاده می شود. فرمول محاسباتی ضریب اسپیرمن-براون به صورت زیر است،
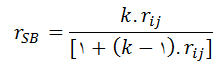
که در آن r_ij ضریب همبستگی پیرسون بین فرم های i وj و همچنین k برابر تعداد کل نمونه تقسیم بر تعداد نمونه در هر فرم است که معمولاً برابر عدد 2 در نظر گرفته می شود.
ضریب گاتمن اصلاح شده ای از ضریب اسپیرمن-براون است که در 6 شکل مختلف L_1 تا L_6 برای اهداف مختلف ارائه می شود. مقادیر ضریب گاتمن به شدت تحت تأثیر نحوه دو نیمه کردن آیتم ها است. یک پیشنهاد اختصاص تصادفی مجموعه آیتم ها به دو گروه است به گونه ای که انتظار می رود واریانس دو مجموعه یکسان باشند.در مورد ضریب گاتمن و اسپیرمن-براون علاوه بر پیش فرض های آلفا فرض های زیر نیز باید رعایت شود :
- اختصاص تصادفی آیتم ها به دو مجموعه .
- همسانی میانگین دو مجموعه: که این پیش فرض در واقع همسان بودن دو مجموع را ارزیابی می کند و برای بررسی آن از آزمون چند متغیره مقایسه میانگین T^2 هتلینگ استفاده می شود.
- همگنی واریانس دو مجموعه: که این پیش فرض برای ضریب اسپیرمن-براون باید برقرار باشد ولی ضریب گاتمن نیازی به برقراری این فرض ندارد.
3-ارزیابی پایایی با روش آزمون-بازآزمون
این نوع ارزیابی پایایی، ثبات اندازه گیری ها در طول زمان را بررسی می کند. از لحاظ آماری، این روش پایایی نسخه ای از پایایی با روش دو نیمه کردن است و برای ارزیابی آن از ضریب اسپیرمن-براون استفاده می شود. از این روی پیش فرض های این روش مشابه روش دونیمه کردن می باشد با این تفاوت که مقیاس مورد نظر در طول زمان ثابت است.
در این روش ارزیابی پایایی لازم است به نکات زیر توجه شود:
1) اجرای دوباره ی آزمون ممکن است مطلوب برخی آزمودنی ها نباشد و این امکان وجود دارد که برخی از آن ها در اجرای دوم شرکت ننمایند و به این ترتیب ریزشی در حجم نمونه روی دهد.
2) این روش برای مقیاس هایی قابل استفاده است که در طول زمان پایدار باشند. برای مثال مقیاس هایی مانند هوش، اضطراب یا افسردگی این ویژگی را دارند ولی سازه ای مانند درد پایدار نیست.
4- ارزیابی پایایی با روش توافق بین ارزیاب ها
در این روش همگنی اندازه گیری ها که توسط یک ابزار روی مجموعه ی واحدی از آزمودنی ها و توسط دو یا چند ارزیاب بررسی می شود، آزمون می گردد تا میزان توافق ارزیاب ها روی ابزار مورد نظر بررسی گردد. برای ارزیابی پایایی با این روش برای داده های اسمی، ترتیبی و کمی به ترتیب از ضریب کاپای کوهن، کاپای وزنی و همبستگی درون رده ای استفاده می شود:
1-4) کاپای کوهن
این شاخص میزان توافق دو ارزیاب را روی یک صفت دو حالتی نشان می دهد. معمولاً عنوان می شود که مقادیر بزرگتر از 0.7 این شاخص، برای این منظور مناسب است.در برخی از منابع نیز مقادیر بین 0.4 تا 0.6 توافق متوسط، مقادیر بین 0.6 تا 0.8 توافق قابل ملاحظه و مقادیر بیش از 0.8 توافق عالی بین دوارزیاب را نشان می دهد.
2-4) کاپای وزنی
این شاخص مشابه کاپای کوهن است با این تفاوت که در این شاخص به رده هایی که مشابه رده مورد بررسی هستند وزن 1 و به رده های نامتشابه وزن صفر اختصاص داده می شود. این شاخص برای بررسی توافق ارزیاب ها در یک مقیاس رتبه ای به کار می رود.
3-4) همبستگی درون رده ای
از این شاخص برای ارزیابی میزان توافق دو یا تعدا بیشتری از ارزیاب ها در اندازه گیری یک متغیر کمی استفاده می شود. برای ارزیابی پایایی اندازه گیری های تکراری روی یک هدف واحد نیز می توان از این شاخص استفاده نمود. این شاخص به عنوان نسبتی از واریانس های درون ارزیاب ها با تکرار اندازه گیری ها به واریانس کل تعبیر می شود.
منبع: روش ها و تحلیل های آماری با نگاه به روش تحقیق. نویسندگان : دکتر ابراهیم حاجی زاده و دکتر محمد اصغری. سازمان انتشارات جهاد دانشگاهی .
دانشجوي گرامي علاوه بر مطالب اين صفحه مي توانيد فيلم آموزش نحوه محاسبه پايايي پرسشنامه -آلفاي کرونباخ در نرم افزار spss و يا در نرم افزار اکسل را در لينک زير مشاهده نماييد:.
آموزش محاسبه پايايي پرسشنامه با spss و Excel






13 دیدگاه. همین الان خارج شوید
سلام. من برای پایان نامه خودم از روش پرسشنامه استفاده کردم. پرسشنامه هایی رو که پخش نموده ام هنگام جمع آوری متوجه می شم که اکثر کارشناسان در پرسشنامه گزینه خیلی کم وکم را تیک می زنند. این سوال برام پیش اومد که نکنه پرسشنامه ام پایایی ش کم بشه.
سلام. نه، اینکه اکثریت پاسخ به گزینه ها چه باشد، تاثیری بر روی پایایی ندارد. بهرحال ممکن است پاسخگویان در زمینه ای اعلام نارضایتی کنند و این مورد جدا از بحث آلفای کرونباخ است.
با سلام
میشه راهنمای بفرمایید تفاوت همبستگی درون رده ای (CCI) با همبستگی درون واحدی (CUI) چی هست
سلام. لطفا به کتاب تحلیل آماری با SPSS مومنی و فعال قیومی مراجعه شود.
با سلام،ایا در روش ازمون باز ازمون اگر پایایی سوالی کمتر از 0/7 باشد باید حذف شود یا میانگین پایایی کل سوالات مدنظر قرار میگیرد؟
سلام. بله حذف یا اصلاح بشه
با سلام
چرا در هیچ متنی به نحوه انجام پایایی اشاره نشده است؟ شنیدم باید پرسشنامه در بازه زمانی دوهفته و دو مرتبه بین تعدادی فرد مشابه جامعه آماری مدنظر توزیع شود. آیا این درست می باشد؟
سلام. همانطور که در این صفحه ملاحظه می کنید، پایایی با روشهای متفاوتی قابل اندازه گیری است که در اینجا توضیح داده شده است.
یکی از روشها، آزمون آلفای کرونباخ است که پیشنهاد می کنم بسته آموزش ویدئویی آنرا از آدرس زیر تهیه و ببینید:
https://www.spss-iran.com/product/cronbach-alpha/
با سلام و تشکر از ارائه مطالب مفیدتون
من میخواستم پایایی پرسشنامه ای رو با آلفای کرونباخ بسنجم حجم نمونه بین 380 تا 400 نفر از دانشجویان و اساتید هستند که باید به این پرسشنامه پاسخ بدن
من قبل از اینکه پرسشنامه رو بین 400 نفرپخش کنم باید با آلفای کرونباخ پایایی رو بسنجم؟
و سوال دیگر اینکه برای آلفای کرونباخ پرسشنامه رو در اختیار چند نفر باید قرار بدم؟
ممنون میشم راهنمایی بفرمایید واقعا به مشکل برخوردم
سلام
ابتدا بایستی پرسشنامه را در اختیار 30 نفر از نمونه خود قرار دهید و داده های این 30 پرسشنامه را وارد نرم افزار نموده و آلفای کرونباخ را محاسبه کنید.
اگر مقدار آلفا بیشتر از 0.7 شد که کار را ادامه می دهید ، اما اگر کمتر شد بایستی پرسشنامه را اصلاح کنید و بعد به پر کردن پرسشنامه ها بپردازید.
آموزش ویدئویی محاسبه پایایی با اکسل و spss را تهیه و استفاده نمایید:
https://www.spss-iran.com/product/cronbach-alpha/
سلام.من برای محاسبه پایایی از روش آلفای کرونباخ داده های طیف لیکرت را وارد نرم افزار spss کردم اما آلفای کرونباخ صفر میشه؟می شه راهنماییم کنین دلیلش چیه؟آیا باید روی داده ها تغییرات خاصی اعمال کنم یا این صفر شدن به دلیل حجم نمونه 25 تایی من است؟ از راهنمایی شما ممنونم
سلام. نه بخاطر حجم نمونه نیست. احتمالا جایی اشتباهی صورت گرفته، مثلا نبایستی سوالات جمعیت شناختی پرسشنامه را در محاسبه آلفای کرونباخ در نظر بگیرید.
یا اینکه ورود داده به نرم افزار به درستی انجام نشده است. پیشنهاد می کنم این آموزش های ویدئویی ما را دریافت و ببینید:
https://www.spss-iran.com/product/spss-data-entry/
https://www.spss-iran.com/product/cronbach-alpha/
سلام وقت بخیر. پرسشنامه ی خودمراقبتی دیابت توبرت روایی و پایایی اش توسط سایر پژوهشگران ایرانی روی دیابت نوع ۲ و بزرگسالان بررسی شده. من میتونم از این پرسشنامه در پژوهش روی نوجوانان دیابتی نوع۱ استفاده کنم؟ یا باید مجدد روایی و پایی اش روی نوجوانان دیابت نوع۱ بررسی کنم؟ (با توجه به این که از این پرسشنامه روی نوجوانان مبتلا به دیابت نوع۱ در خارج از کشور استفاده شده و اولین بار نیست).