هنگامی که در بررسی یک مدل رگرسیونی، متغیر مستقل و رابطه بین آن ها با متغیر وابسته از قبل تعین شده است، پس از تعین معادله رگرسیونی مناسب، ضرایب متغیرها مورد آزمون قرار گرفته و اعتبار مانده نیز سنجیده می شود.

اما در بسیاری از موارد مجموعه متغیرهایی که می بایست در مدل رگرسیون گنجانده شوند از پیش تعین شده نیستند. از این روی غالبا بخش اول تجزیه و تحلیل شامل انتخاب این متغیرها می باشد. در پاره ای از موارد انتخاب متغیرهای مستقل برای ورود به مدل بر مبنای ملاحظات تئوری و یا اصول خاصی انجام می شود، در چنین مواردی نیز مسئله گزینش متغیرها مطرح نیست. اما در مواقعی که نظریه واضحی موجود نیست، گزینش متغیرها برای مدل رگرسیون موضوع مهمی خواهد بود.

در فرمول بندی مدل رگرسیون دو سؤال باید مدنظر باشد. اول اینکه کدام متغیرها باید در مدل قرار گیرند و دوم اینکه چه فرمی از آن ها باید در مدل منظور گردد. به عنوان مثال باید پرسید که آیا متغیر اصلی و یا ترکیبی از این متغیر و شکل تبدیل یافته آن مانند X² یا logX باید در مدل ظاهر شود.

دو نکته مهم در گزینش متغیرها

قبل از بحث پیرامون روش های گزینش متغیرها دو نکته قابل ذکر است:

نخست اینکه صحبت در مورد «بهترین مجموعه متغیرها» که می بایست در مدل گنجانده شوند، معمولا با معنی نیست. به عبارت دیگر بهترین مجموعه متغیرهای کاملا متمایز و مشخص وجود ندارد. از معادله رگرسیون می توان برای اهداف مختلفی استفاده کرد. مجموعه ای از متغیرها که می تواند برای یک منظور مناسب باشند، شاید برای اهداف دیگر بهترین به حساب نیایند. بنابراین هدف استفاده از معادله رگرسیون می بایست در زمان گزینش متغیرها در ذهن باشد.

نکته دیگر آن که چون بهترین مجموعه متغیرها وجود ندارد، ممکن است چندین زیرمجموعه برای تشکیل معادله ارزش یکسانی داشته باشند. یک روش خوب گزینش متغیر معمولا چندین مجموعه مناسب را معرفی می کند نه این که به یک مجموعه منفرد تحت عنوان بهترین مجموعه منتهی شود. مجموعه های مختلف از متغیرهایی که ارزش یکسانی برای تشکیل معادله دارند، ساختار داده ها را روشن ساخته و به درک فرآیند زیربنایی کمک می کند.

موارد استفاده از معادلات رگرسیون

یک معادله رگرسیون می تواند برای اهداف مختلفی استفاده شود که در سه دسته کلی زیر قرار می گیرند:

1. توصیف

معادله رگرسیونی ممکن است برای توصیف فرآیند معینی یا به عنوان مدلی برای توصیف یک سیستم برهم کنشی مورد استفاده قرار گیرد. در مواقعی که توصیف هدف اول است، سعی می شود کمترین تعداد متغیرهای مستقل طوری انتخاب شوند که بخش اعظمی از تنوع در متغیر وابسته را توصیف کنند.

2. برآورد و پیش بینی

گاهی معادله رگرسیونی با هدف برآورد و پیش بینی ایجاد می شود. در این مورد با استفاده از معادله رگرسیون می خواهیم مفدار متغیر وابسته را برای مشاهدات دیگری پیش بینی نموده یا میانگین متغیر وابسته متناظر با مشاهده ی دیگری را برآورد نماییم. وقتی معادله ای بدین منظور استفاده می شود متغیرها طوری انتخاب می شوند که MSE پیش بینی حداقل شود.

3. کنترل

یک معادله رگرسیونی ممکن است به عنوان ابزاری برای کنترل استفاده شود. هدف ایجاد چنین معادله ای ممکن است تعیین مقدار از متغیر مستقل باشد که برای حصول مقدار ویژه ای از متغیر وابسته لازم است. برای این منظور بهتر است ضرایب متغیرها در معادله رگرسیون با دقت بیشتری برآورد شوند.

معیارهای ارزیابی در گزینش متغیرها

1. ضریب تبیین (تعیین)

ضریب تبیین R² معیاری برای اندازه گیری کفایت مدل رگرسیون است که به طور گسترده ای مورد استفاده قرار می گیرد. از نظر محاسباتی این ضریب به صورت زیر نشان داده می شود:

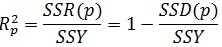
که در آن SSR_p و SSD_p به ترتیب مجموع مربعات رگرسیون و مجموع مربعات مانده ها برای مدل زیرمجموعه p جمله ای هستند.

از آنجایی که مقدار مجموع مربعات رگرسیون با افزایش تعداد متغیرها همواره افزایش می یابد (و در مقابل از مقدار مجموع مربعات مانده ها کاسته می شود) بنابراین همواره با افزایش تعداد متغیرها افزایش می یابد. از این روی استفاده از ضریب تبیین به عنوان معیاری برای انتخاب تعداد متغیر مستقل که بایستی در مدل وارد شوند، درست نیست. اما برای مقایسه دو مدل که دارای تعداد ثابت از متغیرهای مستقل می باشند، می توان از ضریب تعیین فوق استفاده نمود.

2. ضریب تبیین {تعیین} تصحیح شده

برای اجتناب از مشکلات تفسیر برخی از تحلیل گران استفاده از ضریب تبیین تصحیح شده را ترجیح می دهند. این ضریب برای یک معادله p جمله ای به صورت زیر تعریف می شود.

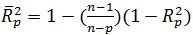
آماره الزاما با اضافه شدن متغیر مستقل به مدل افزایش نمی یابد، بنابراین معیاری برای گزینش یک مدل زیرمجموعه ای مناسب ، انتخاب مدلی است که حداکثر ضریب تعیین تعدیل شده، را داشته باشد.

3. میانگین مربعات مانده ها

از جمله معیارهای دیگر برای قضاوت درباره کفایت مدل برازش داده شده می توان از میانگین مربعات خطا (MSD) نام برد. در یک معادله p جمله ای MSD به صورت زیر تعریف می شود.

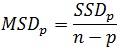
که در آن SSD_p مجموع مربعات مانده ها برای یک معادله p جمله ای است. بین دو معادله، معادله ای که MSD کوچکتری دارد، ترجیح داده می شود. به ویژه اگر برون یابی یا برآورد مقدار متغیر وابسته در خارج از دامنه متغیرهای مستقل مورد نظر باشد. از آنجایی کهSSD_p همواره با افزایش p نقصان می یابد، MSD در ابتدا کاهش یافته، سپس پایدار گشته و سرانجام ممکن است افزایش یابد.

4. آماره C_p مالو

در استفاده از این آماره برای قضاوت درباره یک معادله باید به جای یک میانگین مربعات انحراف از مدل، میانگین مربعات خطای مقدار پیش بینی شده در نظر گرفته می شود. میانگین مربعات خطای پیش بینی استاندارد شده J_p برای داده های مشاهده شده به صورت زیر محاسبه می شود.

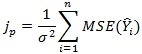
که در آن  MSE میانگین مربعات خطای i امین مقدار پیش بینی شده از یک معادله p جمله ای، و σ² واریانس باقیمانده ها است. برای برآورد j_p از C_p استفاده می شود که تعریف آن چنین است:

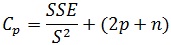
که در آن S² برآورد σ²است. می توان نشان داد که امید ریاضی C_p برابر p است.

این در صورتی است که هیچ اریبی در معادله برازش داده شده با استفاده از p متغیر وجود نداشته باشد. بنابراین انحراف C_p از p را می توان به عنوان معیاری از اریبی مورد استفاده قرار داد. زیرمجموعه ای از متغیرها کهC_pآن ها به p نزدیکتر باشد، زیرمجموعه ای مناسب است.

منبع: مقدمه ای بر تحلیل رگرسیون کاربردی/ نوشته : دکتر عبدالمجید رضایی و مهندس افشین سلطانی/ انتشارات دانشگاه صنعتی اصفهان.

ساير منابع مرتبط با نکات تحليلي آماري :

در خصوص موضوعات مختلف تحليل آماري مي توانيد از مطالب وب سايت ديگر اين گروه نيز استفاده نماييد: مقاله و موضوعات تحليل آماري