روش نمونه گیری خوشه ای
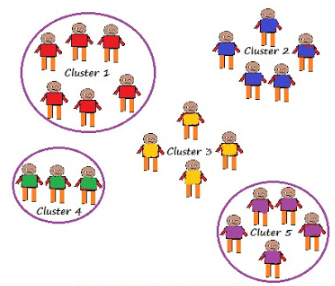
از جمله روش های نمونه گیری که در برخی از موارد مناسب تر از روش نمونه گیری تصادفی ساده عمل می کند، روش نمونه گیری خوشه ای است. یک نمونه ی خوشه ای نمونه ای احتمالی است که در آن هر واحد نمونه گیری مجموعه ای یا گروهی از اعضا است.
دلایل مختلفی برای استفاده از نمونه گیری خوشه ای می تواند وجود داشته باشد. در صورتی که هزینه ی فراهم نمودن یک چارچوب که کلیه اعضای جامعه را فهرست می کند زیاد باشد و یا اگر هزینه فراهم آوردن مشاهدات با افزایش مسافت بین اعضا افزایش یابد، نمونه گیری خوشه ای می تواند کم هزینه تر از نمونه گیری تصادفی ساده یا طبقه ای باشد.
مثال
برای مثال فرض کنید می خواهیم درآمد هر خانوار را در یک شهر بزرگ برآورد کنیم، اگر از نمونه گیری تصادفی ساده استفاده کنیم نیاز به فهرست تمام خانوارهای شهر داریم. یافتن این چارچوب می تواند بسیار پرهزینه و یا غیرممکن باشد، استفاده از نمونه گیری طبقه ای نیز در چنین جامعه ای مستلزم داشتن فهرستی از خانوارها در هر طبقه می باشد. در این حالت می توانیم شهر را به نواحی معینی مانند بلوک ها (خوشه هایی از اعضا) تقسیم نماییم و یک نمونه تصادفی ساده را از بلوک های این جامعه انتخاب کرده و در آمد هر خانوار را در بلوک هایی که در نمونه واقع شده است اندازه بگیریم. این کار با استفاده از یک چارچوب که کلیه بلوک های شهر را فهرست نموده، به اجرا در می آید.
دلیل دیگری که استفاده از نمونه گیری خوشه ای را پیشنهاد می دهد جمع آوری داده ها با هزینه ی کمتر است. برای مثال فرض کنید فهرستی از خانوارهای شهر در دسترس است و می خواهیم نمونه ای به روش تصادفی ساده از خانوارهای مختلف که در سطح شهر پراکنده اند تهیه کنیم. هزینه ی مصاحبه با خانوارها با توجه به هزینه رفت و آمد پرسشگر و دیگر هزینه ها بالا است. یک روش کاهش هزینه های رفت و آمد استفاده از روش نمونه گیری خوشه ای می باشد زیرا افراد درون یک خوشه باید از نظر جغرافیایی به هم نزدیک باشند.
چگونه یک نمونه خوشه ای انتخاب کنیم
اولین مسئله در نمونه گیری خوشه ای انتخاب خوشه های مناسب است. انتخاب مناسب تعداد و حجم نمونه در هر خوشه از اهمیت بالایی برخوردار است. اعضای درون یک خوشه اغلب از نظر فیزیکی به یکدیگر نزدیک اند و در نتیجه تمایل به داشتن خصوصیات مشابهی دارند به عبارت دیگر میزان اطلاعات در مورد پارامتر جامعه ممکن است با نمونه گیری مجدد از یک خوشه تفاوت چشم گیری نداشته باشد. در چنین حالتی یک پژوهشگر ممکن است با انتخاب اندازه ی خوشه ی بسیار بزرگ، تنها پول خود را هدر دهد.
در عین حال موقعیت هایی ممکن است روی دهد که اعضای درون یک خوشه با یکدیگر بسیار متفاوت باشند. در چنین حالتی نمونه هایی که شامل تعداد کمتری از گروه های بزرگ باشد برآورد بسیار خوبی از پارامتر جامعه را بدست می دهد.
مثال
برای مثال فرض کنید در یک نمونه گیری جعبه های حاوی قطعات خارج شده از هر خط تولید به عنوان خوشه ها در نظر گرفته شود. اگر کلیه ی خطوط تقریباً به یک میزان نقص داشته باشند، میزان تغییرات قطعات هر خوشه (جعبه) همان میزان تغییرات جامعه است. در این صورت یک برآورد خوب از درصد قطعات معیوب را می توان با یک یا دو گروه فراهم آورد.
در مقابل فرض کنید که نواحی آموزش و پرورش به عنوان خوشه های خانوارها برای برآورد درصد خانوارهایی که موافق طرح تغییر مرزهای نواحی هستند، در نظر گرفته شود. چون خوشه ها حاوی خانوارهای بسیاری هستند بودجه ی در نظر گرفته شده اجازه انتخاب تنها تعداد محدودی از خوشه ها را می دهد.در این حالت ممکن است در برخی خوشه ها اغلب خانوارها مخالف تغییر نواحی بوده و در مقابل در خوشه ی دیگر اغلب خانوارها از مدارسشان ناراضی بوده و موافق تغییر محدوده ی نواحی باشند. یک نمونه ی کوچک از نواحی ممکن است تعدادی از این مجموعه گروه ها را نادیده بگیرد و بدین وسیله برآورد ضعیفی را نتیجه بدهد. برای رفع چنین مشکلی نمونه گیری از تعداد بیشتری از خوشه ها ولی با اندازه های کوچکتر پیشنهاد می شود.
مقایسه نمونه گیری خوشه ای و طبقه ای
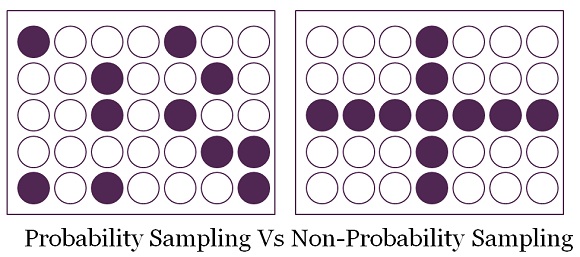
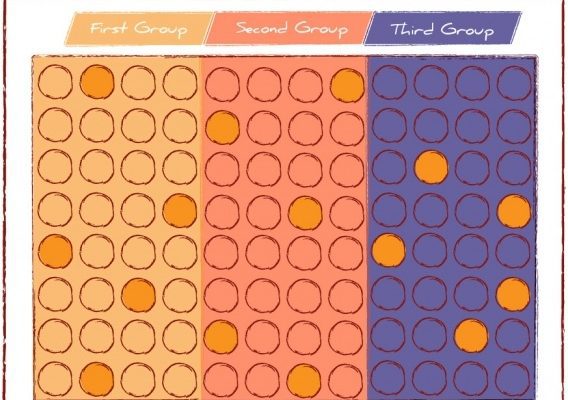
در نمونه گیری طبقه ای ، طبقات تا آنجایی که ممکن است باید از درون به هم شبیه باشند اما یک طبقه باید با طبقه ی دیگر از نظر مشخصه ای که اندازه گیری می شود متفاوت باشد. در نمونه گیری خوشه ای، خوشه ها تا حد امکان باید از درون متفاوت باشند و یک خوشه باید به منظور مزیّت اقتصادی ، بسیار شبیه دیگر خوشه ها به نظر آید.
برآورد میانگین و مقدار کل یک جمعیّت
نمونه گیری خوشه ای یک نمونه گیری تصادفی ساده است که هر واحد نمونه گیری شامل تعدادی عضو است. بنابراین برآوردهای میانگین و مقدار کل جامعه مشابه نمونه گیری تصادفی ساده بدست می آید.
برآوردگر میانگین جامعه ، میانگین نمونه یعنی است:
در این رابطه n تعداد خوشه های انتخاب شده در نمونه ی تصادفی ساده ، تعداد اعضای خوشه ی i ام که در نمونه تصادفی انتخاب شده است و
مقدار کل همه ی مشاهدات در گروه i ام نمونه هستند.
واریانس برآورد شده ی (برآوردگر میانگین جامعه) نیز به صورت زیر است:
در این رابطه
متوسط اندازه تمام خوشه ها برای جامعه است به طوریکه M تعداد اعضای جامعه و N تعداد خوشه ها در جامعه می باشد. همچنين n تعداد خوشه های انتخاب شده در نمونه گیری تصادفی ساده است. لازم به ذکر است که برآوردگر مقدار کل جامعه نیز به کمک رابطه ی
حاصل می شود.
انتخاب حجم نمونه
میزان اطلاعات در نمونه ی خوشه ای از دو عامل تعداد خوشه ها و اندازه ی نسبی خوشه ها تأثیر می پذیرد. تعداد خوشه های که به روش تصادفی ساده باید انتخاب شوند با استفاده از رابطه ی زیر بدست می آید:
که با استفاده از اطلاعات نمونه گیری های مشابه قبلی و یا به کمک یک نمونه ی اولیه و بااستفاده از رابطه ی
برآورد می شود.
منبع : مقدمه ای بربررسی های نمونه ای . نوشته ی شیفر و مندنهال. ترجمه ی دکتر ارقامی ، دکتر بزرگنیا و دکتر سنجری . انتشارات دانشگاه فردوسی مشهد.
براي مشاهده ساير مقاله هاي تحليل آماري اين وب سايت بر لينک زير کليک نماييد: صفحه مقاله هاي تحليل آماري
چنانچه مایلید با انواع روشهای نمونه گیری آشنا شوید این مطلب را در سایت دیگر این شرکت از دست ندهید: روشهای نمونه گیری و تعیین حجم نمونه
آیا می دانید که در این صفحه از سایت ما می توانید: محاسبه آنلاین حجم نمونه با فرمول کوکران را انجام دهید؟







62 دیدگاه. همین الان خارج شوید
سلام. جامعه ی آماری من شامل کارآفرینان شهرک صنعتی یک و دو و همچنین کارآفرینان برتر هستش برای نمونه گیری بهتره از چه روشی استفاده کنم؟
سلام. نمونه گیری تصادفی طبقه ای به نظر مناسب می آید.
به نظر من برای مقاله من که در مورد مادران یک روستاست .روش نمونه گیری خوشه ای مناسبه.
سلام ووقت بخير
ميبخشيد جامعه من از شش مدرسه چهار مدرسه انتخاب كردم كه دوتا پسراته دوتا دخترانه حالا از هرمدرسه كه مقطع دوم متوسطه هستند از هر پايه ورشته يه كلاس انتخاب كردم وپرسش نامه مي خواهم توزيع كنم بايد چه كار كنم روشم تصادفي خوشه اي بايد بقيه كار از قرعه كشي استفاده كنم
سلام. حقیقتش این شیوه نمونه گیری شما به نظر صحیح نیست و احتمالا استاد نیز آنرا قبول نمی کند.
هر انتخابی می بایست منطقی داشته باشد. 6 تا مدرسه از کجا آمده و مربوط به کدام منطقه و شهر است؟ چطور 4 تا انتخاب کردید؟
ابتدا جامعه آماری خود را با دقت تعریف کنید و تعداد آنرا برآورد نمایید. سپس نظام مند به نمونه ها که دانش آموزان هستند برسید.
سلام. من یک پایان نامه در یک شرکت توزیع برق که دارای چند مدیریت برق هست، کار میکنم. و باید به پرسشنامه من سه دسته مدیران، کارشناسان و کارکنان جواب بدن. از چه روش نمونه گیری اسفاده کنم؟ میشه اول خوشه ای و بعد طبقه ای استفاده کرد؟
سلام. از نمونه گیری طبقه ای متناسب با حجم هر طبقه استفاده کنید. حجم نمونه کل را به تناسب حجم جامعه در هر مدیریت برق، تقسیم کنید.
سلام وقتتون بخیر
من با دونفر از دانش اموزان که در مقطع متوسطه اول هستن یک کار پژوهشی رو روی دانش اموزان ناحیه دو مشهد درحال انجام دادن هستیم ،در رابطه با میزان شیوع کوررنکی در بین دانش اموزان این مقطع تحصیلی ،
هشت مدرسه رو انتخاب کردیم بصورت تصادفی چهار تا دخترانه و چهارتا پسرانه
از اونجاییکه کوررنکی درصد کمی از افراد رو در برمیگیره تمام دانش اموزان این مدارس رو در امارگیری شرکت دادیم
این نوع امارگیری رو در چه رشته از انواع امارگیری میشه قرار داد و آیا مورد قبول داور ها قرار میگیره
پژوهش مربوط به جشنواره خوارزمی هست
ممنون میشم راهنمایی کنین منو چون هیچ تجربه ای در این مورد ندارم
سلام. وقت شما هم بخیر. کار شما شبیه به نمونه گیری خوشه ای است. زیرا بعد از انتخاب خوشه (در اینجا مدرسه)، تمام دانش آموزان را در نمونه قرار داده اید.
سلام وقت بخیر
من برای داده هام نمودار خوشه ای و تحلیل عاملی رو انجام دادم… ولی نتایجش با هم یه مقدار متفاوته… این طبیعیه؟؟؟.
که مثلا سه تا عامل که تو یه خوشه بودند حالا تو تحلیل عاملی با گروه دیگه افتاده روی نمودار سه بعدیش
میخواستم بدونم این طبیعیه؟؟؟؟
یا ممکنه روشم مشکل داشته باشه؟؟
ممنون
سلام. بله طبیعیه. چون هر کدوم از روش متفاوتی داده ها رو دسته بندی می کنند.
سلام.
وقتتون بخیر.جامعه آماری من زنان ازدواج کرده ای هستند که سه تا ده سال از ازدواجشان می گذرد و در یک روستای مشخص ساکن هستند، ممنون میشم واسه نمونه گیری راهنمایی بفرمایید.
سلام. به نظر نمونه گیری در دسترس (اتفاقی) است. به تصادف به هر خانمی که برخورد نمودید و سه تا ده سال از ازدواجش گذشته بود، به سوالات شما پاسخ دهد. این صفحه را مطالعه نمایید:
https://spss-iran.ir/NonProbabolitySampling.php
سلام خسته نباشید
می خواستم درمورد محاسبه خطای نمونه گیری در روش خوشه ای توضیحی بدهید
سلام و خدا قوت. این مبحثی پیچیده است. لطفا به کتابهای نمونه گیری مراجعه نمایید.
سلام : میخواهیم میزان رضایت کارمندان یک وزارت را ازرهبری وزارت سنجش یا معلوم نمایم ،
لطف نموده کمک نمایید که ازکدام روش تحقیق استفاده نمایم لطفآ.
این ایمل اول من است
سلام بر خواهر گرامی، خوشحالم که در کشور افغانستان نیز مطالب این سایت مورد توجه قرار می گیرد.
شما لازم است ابتدا حجم نمونه را با توجه به تعداد کل کارمندان آن وزارت خانه بر اساس فرمول کوکران بدست آورید. از این لینک در سایت دیگر این شرکت : محاسبه انلاین حجم نمونه با فرمول کوکران
شیوه نمونه گیری نیز به نظر من اینطور باشد، اما نظر استاد شرط است: ساختمان ها یا دپارتمان های مختلف این وزارت خانه را به عنوان طبقات در نظر بگیرید و به تناسب تعداد کارمندان آن دپارتمان ها، حجم نمونه را تخصیص دهید. یعنی نمونه گیری طبقه ای انجام دهید.
سلام
تفاوت میان نمونه گیری تصادفی طبقه بندی شده و خوشه ای چیست؟
با تشکر تمام لطفاً پاسخ بدهید
سلام
اگه بخوایم یه دانشگاه رو با در نظر داشتن پردیس های دانشگاه، دانشکده ها و بعد کارکنان بررسی کنیم. میشه بفرمایید خوشه پردیس هست یا دانشکده ها
سلام. در خوشه بایست همه جور جنسی داشته باشیم. در این مورد خوشه وجود ندارد. پردیس و دانشکده ها طبقه هستند.
با سلام و احترام
موضوع پایان نامه دوره کارشناسی (سال 86) بنده “بررسی رابطه شخصیت برونگرا و درونگرا با میزان هیجان خواهی در دختران مقطع دبیرستان منطقه 16 تهران” بوده است. لذا 4 مدرسه انتخاب و در هر مدرسه تعدادی کلاس جهت توزیع پرسشنامه ها برگزیده شدند. در آن زمان با راهنمایی استاد مربوطه روش نمونه گیری “تصادفی” ذکر شده که با اطلاعات حال حاضر، تقریبا مطمئن هستم این نمونه گیری تصادفی نبوده… لازم به توضیح است تعداد جامعه آماری (کلیه دانش آموزان دختر مقطع دبیرستان منطقه 16 تهران) 5947 نفر بوده و تعداد نمونه هم 149 نفر در نظر گرفته شده… که تعداد نمونه هم اکنون محل سوال است…
از آنجاییکه اکنون قصد چاپ مقاله ای (در مجله علمی-تخصص) از همین پایان نامه را دارم، ممنون میشم در خصوص دو مورد ذکر شده (نحوه نمونه گیری و تعداد نمونه) راهنمایی بفرمایید تا آن را اصلاح کنم…
با تشکر فراوان
سلام. روش شما شبیه نمونه گیری طبقه ای است.
سلام من یه جامعه 7500 نفری دارم به نظرتون از چه روش نمونه گیری باید استفاده کنم همچنین چه تعداد را در بر میگیرد . مرسی
سلام. از فرمول کوکران استفاده کنید. در این صفحه سایت دیگر ما به صورت آنلاین می توانید حجم نمونه را حساب کنید با فرمول کوکران:
https://www.spss-iran.com/sample-size/
با سلام وقت بخیر پایان نامه من در مورد کارکنان بیمارستان شهر هرمزگان است از روش نمونه گیری خوشه ای چند مرحله ای باید استفاده کنم؟8 تا بیمارستان داره دو تا رو از این روش انتخاب کردم ولی نمیدونم توضیح و دلیلش چی میشه؟
سلام. به نظر من بهتر است از طبقه ای استفاده کنید و از هر بیمارستان به تناسب جمعیت کارکنان آن نمونه ای بردارید.
سلام و وقت به خیر، راجع به سوال خانم یاسمن در بررسی رابطه بین شخصیت های برون گرا و درون گرا با میزلن هیجان خواهی در دبیرستان های منطقه ۱۶، شرایط از نظر همگنی بین و ناهمگنی درون دسته ها( دبیرستان ها) مناسب روش خوشه ای هست اما به دلیل عدم بررسی کلیه دانش آموزان چهار دبیرستان منتخب، روش شبیه به طبقه ای شده، درسته؟
یا از نظر نظر همگنی درون دبیرستان ها و ناهمگنی بین دبیرستان ها مناسب روش طبقه ای تشخیص دادید؟؟؟
سلام. بله. زیرا در خوشه ای وقتی یک خوشه انتخاب شد لازمه کل آن برداشت شود.
سلام. من جامعه ی آماریم، اعضای سمن های زیست محیطی استان مازندران است. استانداری ۲۶ سمن را معرفی کرد که فقط ۱۹ سمن با من همکاری کردند. کل اعضای این ۱۹ سمن ۱۱۲۲ نفر بودند که با توجه به جدول مورگان ۲۸۶ نفر برای نمونه محاسبه شد. به نظر شما نمونه گیری از چه نوعی می شود؟
سلام. به نظر من طبقه ای. یعنی از هر سمن به تناسب جمعیت آن نمونه بگیرید. اگر سخت است ابتدا به تصادف تعدادی سمن انتخاب و بعد در سمن های انتخابی به تناسب جمعیت آن، نمونه بگیرید.
سلام دوباره. ممنون از راهنماییتون. حال اگر تعداد دقیق اعضای این ۱۹ سمن را ندانیم، از چه روش نمونه گیری باید استفاده کرد؟. و یک سوال دیگر اینکه از چه راه هایی می توان متوجه شد که سطح تحلیل فرد است یا سازمان؟
سلام. چارچوب و دانستن برآوردی از تعداد اعضای سمن ها لازم است در نمونه گیری طبقه ای. برآورد کنید.
ممنون از شما. خیلی بزرگوارید.
سلام خطای محرز در نمونه گیری خوشه ای چیست؟؟؟
سلام. اینکه با نمونه گیری طبقه ای اشتباه گرفته شود.
در نمونه گیری طبقه ای، در داخل هر طبقه حداکثر همگنی وجود دارد.
سلام .موضوع من بررسی رابطه دینداری و رضایت سیاسی بین شهروندان یه شهرستان 500هزار نفری. از فرمول کوکران384 نمونه انتخاب شدند و استاد توصیه کرده با استفاده از نقشه سکونت گاهی، از روش طبقه بندی چند مرحله ایی استفاده بشه .آیا این شیوه درستی هست؟ممنون میشم دربارش راهنمایی کنید
سلام. بله درست گفتند. زیرا شهر به مناطق و نواحی ای تقسیم بندی می شود که معمولا همگنی بیشتری بین نظرات افراد ساکن در یک ناحیه وجود دارد (با توجه به نزدیکی سطح اجتماعی و درآمدی آنان). و حجم نمونه نیز به تناسب جمعیت هر منطقه یا ناحیه تقسیم بندی شود. اینطوری به صورت عادلانه از تمام مناطق شهر نمونه گیری شده است. نه اینکه مثلا فقط از مناطق مرفه شهر نظرسنجی شود.
سلام وقتتون بخیر
نمونه گیری تصادفی ساده و نمونه گیری خوشه یک مرحله ای وقتی حجم خوشه ها با هم برابر نیست مقایسه کنید
ممنتون میشم که با توضیح کامل و درست منو راهنما کنید
سلام. فرق شون اینه که در نمونه گیری تصادفی ساده، مفهومی به نام خوشه نداریم که بیاییم تعدادی خوشه را انتخاب کنیم و بعد داخل خوشه ها، سرشماری داشته باشیم.
سلام، وقت بخیر.
موضوع پایان نامه اینجانب در رابطه با مصرف آب مدارس است. نیاز دارم که یکسری از مشترکین مصرف کننده آب(مدارس) را انتخاب کنم و برای جمع اوری اطلاعات تکمیلی در میان آنها پرسشنامه پخش کنم. میزان مصارف و مناطق و مقطع تحصیلی مدارس متفاوت است. از چه روش نمونه گیری باید استفاده کنم؟
ممنون میشوم لطف کنید راهنماییم کنید.
سلام. نمونه گیری طبقه ای به نظر مناسب میاد. جامعه آماری تان را به طبقاتی تقسیم بندی کنید (مثلا نواحی آموزش پرورش) و بعد به تناسب حجم آن، از داخل هر کدام نمونه گیری شود.
باعرض سلام میخوام درموردیه موضوعی تحقیق کنم میخوام راهنمایی بفرمایید.موضوع تحقیق تعدادافرادبیسوادیاکم سواددریک استان است لطفا مراحل شروع رابهم بگیدوراهنمایی بفرمایید
سلام. به آمارهای رسمی و مرکز آمار ایران مراجعه داشته باشید. به نظر در سرشماری ها، تحصیلات پرسیده شده است.
سلام جامعه من معلمان دوره متوسطه اول ودوم دریک شهرستان است نمونه گیری من ازچه نوعی است
سلام. به نظر طبقه ای مناسب کار شماست
میشه یک مثال برای نمونه گیری طبقه بندی وخوشه ای بگین؟
سلام و عرض ادب
پژوهش بنده در مورد کیفیت مترو هست و احتیاج به پرسشنامه جهت نظرخواهی ( مدل سروکوال) دارم، به نظر شما روش نمونه گیری تصادفی ساده مناسب هست یا باید از روش خوشه ای استفاده کنم؟ ممنون.
سلام. برای اینطور امور که پیچیدگی دارد، روش نمونه گیری تصادفی ساده خیلی مناسب نیست.
نمونه گیري خوشه ای دو مرحله ای طبقه بندی شده ایا همچین مدلی وجود دارد و یعنی چه
یاخوشه ای یا طبقه بندی شده دیگه. دو تا با هم که نمیشه
سلام،جامعه آماری من دانش آموزان تیزهوش دبیرستانی هستش،از کدام روش نمونه گیری باید استفاده کنم؟
سلام . نمونه گیری طبقه ای. البته بایستی دانش آموز تیز هوش را دقیقا تعریف کنید که کیا هستن.
با سلام
در صورتیکه بخواهم دانش و نگرش نسبت به کارگاههای برگزار شدهی خاصی را در کشور بدانم، چه نوع نمونه گیری را پیشنهاد می دهید:
سلام. نمونه گیری در دسترس، که یک روش نمونه گیری غیر احتمالی است. زیرا دسترسی به این کارگاه ها عملا مشکل است.
سلام جامعه آماری من دانش آموزان ابتدایی شهر تهران هستند و نمونه رو نوشتم کلاس هایی از مدارس ۵ منطقه از تهران که تصادفی انتخاب میشوند و نمونه گیری هم نوشتم از ۵ گروه منطقه تهران از هر منطقه ۲ تا مدرسه ابتدایی از هر دبستان ۲ کلاس را تصادفی انتخاب میکنیم ولی شک دارم درسته یا نه؟ و نمونه رو نمیدونم بطور دقیق چی باید بنویسم میشه بگید نمونه رو چی بنویسم و نمونه گیری خوشه ای که نوشتم درسته؟؟
سلام . به نظر نمونه گیری طبقه ای انجام شده نه خوشه ای
با سلام، موضوع پژوهش بنده زنان شاغل متاهل سازمانهای دولتی در یک استان هست، برای روش نمونه گیری راهنمایی میفرمایید؟
سلام. بستگی به روش تحقیق دارد. اما یک پیشنهاد می تواند این باشد که در هر سازمان را یک طبقه در نظر بگیرید و بعد به تصادف در هر سازمان افرادی را انتخاب نمایید. یعنی نمونه گیری طبقه ای را انجام دهید.
با سلام تفاوت نمونه گیری خوشه ای با نوع سهمیه ای نمونه گیری درچیست؟
سلام. مهمترین تفاوت شان این است که نمونه گیری سهمیه ای، نمونه گیری غیر احتمالی است اما نمونه گیری خوشه ای از نوع احتمالی است. این صفحه را هم مطالعه نمایید:
https://spss-iran.ir/NonProbabolitySampling.php
سلام و خسته نباشید.
جامعه اماری من بیمارانی هستند که در پزشک خانواده شهری پرونده دارند.
من اول میخوام مثلا از بین 100 پزشک 30 تا انخاب کنم و بعد از هر پزشک 10 بیمار لز چه روشی باید استفاده کنم؟
با تشکر
سلام. باید ببینید برای انتخاب پزشک یا بیماران چه اطلاعاتی در دست دارید و چطور می توانید جامعه خود را طبقات مختلفی تقسیم بندی کنید. آنگاه در یک یا دو مرحله به صورت طبقه ای انتخاب نمونه را انجام دهید.
مثلا ممکن است محل سکونت (منطقه شهرداری) یک آیتم طبقه بندی باشد.